A manifold is a continuous space whose points can be assigned coordinates, the number of coordinates being the dimension of the manifold [ for example a surface of a sphere is 2D, spacetime is 4D ].
A manifold is differentiable
if we can define a scalar field 
at each point which can be
differentiated everywhere. This is always true in Special Relativity
and General Relativity.
We can then define one- forms 
as having components 
and vectors 
as linear functions
which take into the derivative of along a
curve with tangent :
Tensors can then be defined as maps from one- forms and vectors into the reals [ see chapter 3].
A Riemannian manifold is a differentiable manifold with a symmetric metric tensor g at each point such that
for any vector for example Euclidian 3D space .
If however 
is of
indefinite sign as it is in Special and General Relativity it is called Pseudo- Riemannian.
.
For a general spacetime with coordinates 
, the
interval between two neighboring points is
In Special Relativity we can choose Minkowski coordinates such
that 
everywhere. This will
not be true for a general curved manifold. Since 
is a symmetric matrix, we can always choose a coordinate system
at each point 
in which it is transformed to the
diagonal Minkowski form, i.e. there is a transformation
such that
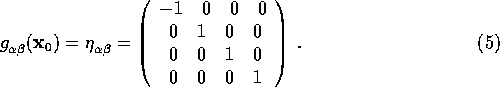
Note that the sum of the diagonal elements is conserved; this is the signature of the metric [ +2 ].
In general 
will not diagonalize
at every point since there are ten functions
and only four transformation
functions 
.
We can also choose so that the
first derivatives of the metric vanishes at i.e.
for all 
, 
and 
. This implies
That is, the metric near is approximately that
of Special Relativity, differences being of second order in the
coordinates. This corresponds to the local inertial frame whose
existence was deduced from the equivalence principle .
In summary we can define a local inertial frame to be one where
for all , ;
for all , , ; however
for at least some values of , , and
.
It reflects the fact that any curved space has a flat tangent space at every point, although these tangent spaces cannot be meshed together into a global flat space.
Recall that straight lines in a flat spacetime are the worldlines of free particles; the absence of first derivative terms in the metric of a curved spacetime will mean that free particles are moving on lines that are locally straight in that coordinate system. This makes such coordinates very useful for us, since the equations of physics will be nearly as simple as they are in flat spacetime, and if they are tensor equations they will be valid in every coordinate system.